Boolean Algebra Calculator is a tool that helps you simplify logical expressions easily using basic rules of Boolean algebra.
Instead of solving long expressions by hand, you can just enter them into this calculator—like (A + B)(A + !B)(!A + C)—and it will….
- Show you the Boolean algebra simplification result
- Generate the truth table
- Give you SOP (Sum of Products) and POS (Product of Sums) forms
- Explain the steps clearly
How to Use Boolean Algebra Calculator ?

- Enter Your Boolean Expression, In the input box, type your Boolean expression. You can use….
⊕for XOR (optional)+for OR•for AND (or simply write two variables together likeAB)!AorA'for NOT A()for grouping terms
For Example : (A + B)(A + !B)(!A + C)
2. Then Click on Calculate
3. What Will Be the Outputs?
Once Simplify Boolean Expressions Online, you will get Output as
Simplified Expression (Y = …) : A shorter version of your input using Boolean rules.
For example: A•C
Truth Table : A table that shows every possible input combination and the result (0 or 1) for each.
SOP (Sum of Products) : A form where output is 1, written as OR of multiple AND terms.
Example: A•!B + !A•C
POS (Product of Sums) : A form where output is 0, written as AND of multiple OR terms.
Example: (A + B)(!A + C)
Sharing Options : You can share the result on WhatsApp or Email directly, with one click.
Boolean Algebra Calculator
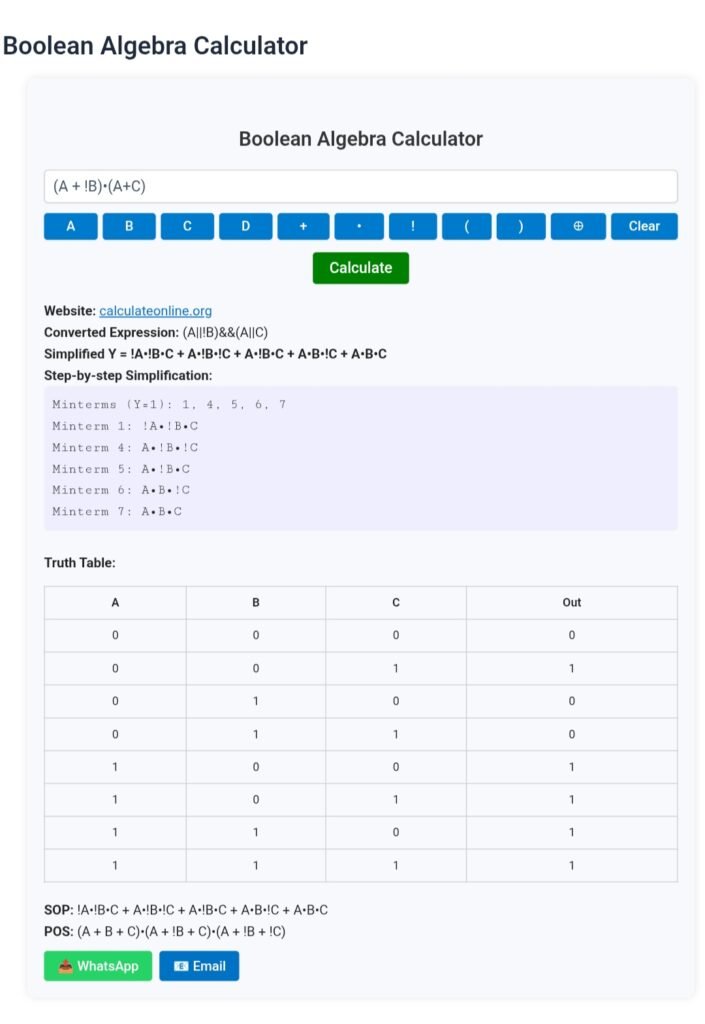
Examples of Boolean Expressions and Results
Below are the result of Boolean Algebra Simplification, by choosing Boolean Expression Simplifier
- (A + B)(A + B̅)(A̅ + C)
- Simplified Expression (Y):
A•C - SOP (Sum of Products):
A•C - POS (Product of Sums):
(A + B)(A + !B)(!A + C) - Truth Table
| A | B | C | Y (Output) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
2. (A + B’) • (B + C)
- Simplified Expression (Y):
A•C + B'•C + A•B - SOP:
A•C + B'•C + A•B - POS:
(A + !B)(B + C) - Truth Table
| A | B | C | Y (Output) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
What is Boolean Expression Simplification?
Boolean simplification means reducing a Boolean expression into its simplest form using algebraic rules, Karnaugh Maps, or truth tables without changing its output. The simplified expression uses fewer gates and is more efficient in digital circuits.
Why Simplify Boolean Expressions?
- Reduces the number of logic gates in circuits.
- Saves cost, power, and space.
- Improves performance in hardware and software.
- Makes the logic easier to understand and debug.
Methods to Simplify Boolean Expressions
1. Algebraic Method :
Use Boolean algebra laws to simplify expressions step-by-step.
2. Karnaugh Map (K-Map):
A visual method using a grid to group 1s and minimize expressions.
3. Truth Table Method:
Build a truth table, find equivalent expressions and reduce.
Boolean Laws & Identities (You can Used in All Methods)
| Law | Expression |
|---|---|
| Identity Law | A + 0 = A ; A · 1 = A |
| Null Law | A + 1 = 1 ; A · 0 = 0 |
| Idempotent Law | A + A = A ; A · A = A |
| Involution Law | (A’)’ = A |
| Complement Law | A + A’ = 1 ; A · A’ = 0 |
| Distributive Law | A(B + C) = AB + AC |
| Absorption Law | A + AB = A ; A(A + B) = A |
| DeMorgan’s Law | (A·B)’ = A’ + B’ ; (A + B)’ = A’·B’ |
1. Algebraic Method Step by Step with Example
Example:
Simplify: F = A·B + A·B'
Step 1: Apply Distributive Law
Take out A as common:
F = A·(B + B')
Step 2: Apply Complement Law
B + B’ = 1
F = A·1
Step 3: Apply Identity Law
A·1 = A
F = A, Final Simplified Expression: F = A
Example: F = AB + A'B
Step 1: Use Distributive Law (Group by B)
F = B(A + A')
Step 2: Apply Complement Law
A + A’ = 1
F = B·1
Step 3: Identity Law
F = B
Simplified: F = B
2. Karnaugh Map (K-Map) Method
When to Use:
- Best for 2 to 4 variables
- Easier for visual grouping
Example:
Simplify this expression:
F(A, B) = Σ(1,2,3)
Step 1: Create Truth Table
| A | B | F |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Step 2: Draw 2-variable K-Map
B A
0 1
———–
0| 0 1
1| 1 1
Step 3: Group Adjacent 1s
We can form a group of three 1s: cells (1,2,3)
- Group 1 (B=1): Cells (1,3)
- Group 2 (A=1): Cells (2,3)
Step 4: Write Minimal Expression
- Group 1 → B
- Group 2 → A
F = A + BSimplified: F = A + B
3. Truth Table + Comparison
Expression:
F = AB + A’B
Build the truth table:
| A | B | AB | A’B | F |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
Now we try to match the outputs–>
1 at rows (A=0,B=1) and (A=1,B=1)
So minimal expression is: B
F = B (Same result as in algebra)
Examples
Example 1:
Simplify: F = A + ABApply Absorption Law: F = A
Example 2:
Simplify: F = A·B + A·C + B·C
Summary Table of Simplification
| Expression | Simplified | Method Used |
|---|---|---|
| A·B + A·B’ | A | Algebraic (Common term) |
| AB + A’B | B | Algebraic (Factoring) |
| A + AB | A | Absorption Law |
| A + A’B | A + B | Algebraic & DeMorgan |
| Σ(1,2,3) | A + B | Karnaugh Map |
Why SOP and POS Are Useful?

SOP (Sum of Products) and POS (Product of Sums) are ways to simplify your Boolean expression.
Why is simplification important? 1. It’s easier to solve questions in exams or build digital circuits practically
2. It helps you understand the logic more clearly
3. It makes your circuit design smaller and faster
Other Calculators :
- Energy Saving Cost Calculator
- Boolean Algebra Calculator
- Geothermal Cost Calculator
- Old Phone/Mobile Cost Calculator
- BigQuery Cost Calculator
- Solar Pump Cost Calculator
- Solar Calculator India
FAQs
What is the role of Boolean Algebra in digital electronics
Boolean Algebra is like the language of digital electronics. It helps us write, simplify, and understand how digital circuits work using just 1s and 0s.
Can I simplify expressions with 4 or more variables?
Yes, the calculator supports multiple variables like A, B, C, D, and even more. It automatically generates the full truth table and shows the simplified output for any expression.
What is Boolean algebra used for
Use of Boolean Algebra : 1.Digital Electronics and Circuit Design, 2.Simplifying Logical Expressions, 3.Programming and Algorithms, 4.Computer Science and AI, 5.Mathematics (Discrete Math).
What is 1+1 in Boolean algebra
Boolean Algebra 1 + 1 = 1
1+1=1 Theory name
In Boolean Algebra , 1+1=1
a’+1 in Boolean algebra
Any value OR 1 = 1, so A’ + 1 = 1
a + a’b = a+b in Boolean algebra
a + a’b = a + b is absolutely correct. You can check it in calculator by adding left and right expression one by one
A’B+AB’ simplify
This is a classic expression known as the Exclusive OR (XOR) function. This matches the output of A ⊕ B. You can check in above Boolean Algebra calculator.
(A+B)(A+B’) Boolean
(A + B)(A + B′) = A+BB’ = A
